Difference between revisions of "An introduction to ship stability"
Acelanceloet (talk | contribs) (→Estimating the center of gravity of an existing ship using the stability) |
Acelanceloet (talk | contribs) (→Rules of thumb for modifying a ships stability) |
||
| Line 121: | Line 121: | ||
==Rules of thumb for modifying a ships stability== | ==Rules of thumb for modifying a ships stability== | ||
| + | It is not always necessary to make a full calculation of a ships stability. For small changes to an calculated or existing design or to the load conditions of a ship, some rules of thumb can be followed to find the effects on the ships stability. | ||
| + | * Any change in the height of the center of gravity will have an opposite effect on the metacentric height. So moving the center of gravity one meter up means the metacentric height comes down one meter. | ||
| + | * On a given waterline shape and size, an increase of block coefficient (more volume under water) means an lower BM so a reduced metacentric height. With an higher block coefficient on a given waterline it is not unlikely that KB will also end up lower below the waterline, further decreasing metacentric height. This change is normally not that big and often comes with an decrease of the center of gravity height as well, offsetting this factor somewhat. | ||
| + | * Increasing the ships waterline size, especially the ships beam, will increase BM and with that the ships metacentric height. | ||
| + | * Raising the center of buoyancy (often visible in a reduction of midship coefficient) increases metacentric heights. | ||
| + | * Metacentric heights is between 1 and 2 meters for almost every ship of every size, apart from special cases (pontoons, crane barges, semi-submersibles, very small ships, etc) where there are special requirements or relatively large changes in center of gravity that have to be offset by a much larger stability margin. | ||
| + | |||
| + | |||
[[Category:Articles]] | [[Category:Articles]] | ||
Revision as of 09:26, 1 May 2022
--- Coming soon ---
--- work in progress below ---
Note: there may be words and definitions which might not be familiar to everyone in this article. Please take a look at the bucketeers glossary Bucketeers Glossary or contact acelanceloet on discord or by forum pm if any questions remain (which I will then answer and add to the bucketeers glossary)
This article is written by J. Scholtens / acelanceloet to provide some insight in the stability of ships, how it impacts ship design and how to use some simple calculations and estimations to see if your shipbucket drawing would stay upright, safe and comfortable. Each section is in theory independent, you can read just the section of what you want to do (for example, estimate the center of gravity of an real ship so you can compare it with your AU design) but to fully understand what you are doing and why it works, it may be required to read the sections above it. That way, I hope that this article will be useful for the people who want to do full calculations, but also for the people who just want to do a quick estimate if their ship works. Unless stated otherwise, I will be using SI units (mostly meters).
Currently, this article remains a work in progress. Reach out to me on discord or on the forums in case you have corrections or questions.
Contents
- 1 Definitions
- 2 Archimedes' law: Why objects float
- 3 The simple case: Stability of an submerged object
- 4 Stability while afloat at the surface
- 5 Calculating the metacentric height
- 6 The stability curve
- 7 Stability requirements
- 8 Estimating the center of gravity of an existing ship using the stability
- 9 Rules of thumb for modifying a ships stability
Definitions
- The ship: the floating object we are doing these calculations for. I will be using ship, but a boat, bouy, submarine or a pontoon of course follows the same rules.
- 'K' : The zero point for the Metacentric height calculation. It can be chosen to be any point, as long as it is constant in the calculations. Normally, it is kept at the bottom of the ship, the keel, which is why the K is chosen for it's abbriviated form.
- 'G' : The Center of Gravity of the ship, or in other words the balancing point of all weights on the ship combined.
- 'B' : The Center of Bouyancy of the ship. This is the center of gravity of the water displaced by the ship, or in other words the centerpoint of the underwater volume of the ship.
- 'V' : The volume of the ship. Following archimedes' law, this is equal to the weight of the ship divided by the density of the water.
- 'KG' : The distance between K and G in vertical direction.
- 'KB' : The distance between K and B in vertical direction.
Archimedes' law: Why objects float
There is a direct relation between submerged volume and weight of an object. If a bucket of water is filled to the brim and a floating object is put in, some water will flow over the edge of the bucket. Interestingly, the weight of this water will be the same as that of the floating object. Due to the fact that the density of water is known, a relation between the displaced water and the submerged volume of the object can also be found. Because the floating object 'displacing' the water that otherwise would be in that location, a ships weight is often stated as displacement
The resulting formula is:
- displacement = underwater volume * water density
or in symbols
- Δ = V * ρ
Water density is 998 kg/m3 for fresh water and 1025 kg/m3 for salt water. Due to the closeness to 1000 of both values, for estimations displacement in cubic metres is often stated as being equal to displacement in metric tons. This of course isn't valid in detailed calculations, although for fresh water it is considered close enough in many cases.
Using Archimedes' law the submerged volume of a ship can be found if the weight is known, or a weight can be found when the volume is known. This forms the basis for the stability calculation: with this it is proven that displacing water by pushing something into it delivers an opposing force equal to the weight of the water it 'replaces'.
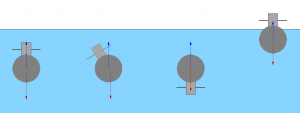
The simple case: Stability of an submerged object
Below the surface of the water, stability is relatively simple. The best example of this case is an submarine. In an object completely submerged in a single medium, it will be stable if the center of gravity is directly below the center of bouyancy. If the object starts to slant, the center of gravity moves to the side of the center of bouyancy, creating an counterforce that gets bigger the more the larger the angle of the object becomes. This counterforce reaches zero when the angle returns to zero. In that essence, the further below the center of gravity is below the center of bouyancy, the larger this counterforce becomes with every angle.
Submarines are well known for their uncomfortable motions at the surface. This can be explained when looking at the characteristics of objects floating at the surface.
Stability while afloat at the surface

On the surface, the stability of an floating object follows the same laws as below the surface with one addition: the shape of the objects submerged volume changes as the object gets an angle. one side is lifted out of the water while the other is pushed deeper into it. The center of gravity moves over a bit to the low side, but the center of bouyancy does so too due to the loss of volume at the high side and the increase of volume at the low side. In other words: at the surface, as long as the shape of the waterline remains the same, the bigger the angle gets, the more the objects volume starts counteracting. So, a ship at the surface is a lot more stable then a submerged object.
To find out how stable, it is required to do some calculations, which can be found in the next paragraph. It is however possible to do some simple estimations:
- The lower the center of gravity, the higher the stability
- The lower the volume relative to the waterline area, the higher the stability.
- The higher the center of bouyancy, the higher the stability.
- The larger the ships beam, the larger the ships stability.
Calculating the metacentric height
To really compare a ships stability, it is required to do calculations though. The most important value to compare stability of ships is the metacentric height or GM. Metacentric height is a fictional turning point for the angling of the ship. The center of gravity of the ship can be considered a pendulum that is attached at this fictional point, the metacentre. This means that the higher this GM gets, the slower the ship angles and the more momentum is needed to get it to heel.
A high GM thus means that it is difficult to get the ship to heel over. Interestingly, GM doesn't scale linearly with ship size: a sailing yacht and a panamax container ship might have metacentric heights which are not very far apart. How to compare the requirements set for metacentric heights will be described in the paragraph #Stability requirements
The formulas used for the calculation of the metacentric height are the following:
- GM = BM + KB - KG
in which:
- BM = Iwp / V
BM is the distance between the Center of Bouyancy and is defined by the second moment of inertia of the shape of the waterline divided by the underwater volume of the ship. More about the second moment of inertia below. The BM is the reason the stability goes up if the volume of the ship is reduced without changing the waterline and also the reason why stability goes up when stability rises when the waterline area is increased without changing the ships volume.
The GM, KB and KG are described earlier on this page.
Second moment of Inertia of the ships waterline
The second moment of inertia of the waterline is the most complicated part of the stability calculation. It is a value for the waterline area and the distribution of that area. For simple shapes, a formula can describe it exactly:
- Rectangle: IWP = 1/12 * L * B3
- Oval: IWP = 1/4 * Pi * (0.5 * L) * (0.5 * B)3
The above formula's are valid for transverse stability. Longtitudinal stability uses the same formula's but of course a ship pitches a lot harder then it heels in most cases. Center of bouyancy, center of gravity and the volume remain the same, but the second moment of intertia is modified to perform this mechanic: the longtitudinal second moment of inertia is defined by moving the cubed factor to the length instead of the beam, so for the rectangle that results in:
- Rectangle: 1/12 * B * L3
In the table below a few waterline second moment of inertia formula's are coupled with an waterplane coefficient and a description of the hulls. They are all estimations so be careful when applying them to real designs but they will work to get an estimation of stability of a ship.
| Shape / ship type | IWP = | Waterplane coefficient |
|---|---|---|
| Square pontoon | 1/12 * L * B3 | 1.00 |
| FPSO (rounded pontoon shape) | 1/13 * L * B3 | 0.95 |
| Heavy lift ship (sharp bow, parallel midship, broad transom stern) | 1/15 * L * B3 | 1.00 |
| Bulkcarrier (round bow, small transom stern) | 1/16 * L * B3 | 1.00 |
| Modern warship hull | Between 1/16 and 1/24 * L * B3 | Between 0.84 and 0.72 |
| Cruiser hull (sharp bow, small transom) | 1/22 * L * B3 | 0.75 |
| Semi-planing hull | 1/22 * L * B3 | 0.75 |
| Sailing yacht (sharp bow, sharp or rounded stern) | Between 1/20 and 1/26 * L * B3 | Between 0.79 and 0.67 |
| Container ship (sharp bow, small or no transom) | Between 1/22 and 1/26 * L * B3 | Between 0.75 and 0.67 |
| Planing hull | 1/26 * L * B3 | 0.67 |
| Pre-war destroyer hull | 1/26 * L * B3 | 0.67 |
Note that the faster a ship will go (relative to it's size) the less the hull is optimised for stability and the more for speed, leading to a lower waterplane area second moment of inertia and with that to a lower BM.
The stability curve
Stability requirements
Estimating the center of gravity of an existing ship using the stability
Using the above formula’s and information, it is possible to estimate the stability of any ship design. However, one factor is often somewhat hard to estimate, which is the height of the center of gravity. There are 2 ways to estimate the center of gravity of a ship:
- Take the center of gravity height above the keel of every component and multiply this with the weight of this component. Then take the sum of all multiplied components and divide this by the total weight ( = the displacement of the ship)
- Estimate (possibly by using the above method) how the center of gravity differs from a reference ship of which the metacentric height and dimensions are known. Then reverse engineer the metacentric height of that ship (calculating BM and estimating KB) to find KG.
The last method is one more commonly used in initial or conceptual design (if the center of gravity cannot be estimated from earlier similar projects, that is)
The formula to be used to find the KG is: KG = BM + KB – GM
Rules of thumb for modifying a ships stability
It is not always necessary to make a full calculation of a ships stability. For small changes to an calculated or existing design or to the load conditions of a ship, some rules of thumb can be followed to find the effects on the ships stability.
- Any change in the height of the center of gravity will have an opposite effect on the metacentric height. So moving the center of gravity one meter up means the metacentric height comes down one meter.
- On a given waterline shape and size, an increase of block coefficient (more volume under water) means an lower BM so a reduced metacentric height. With an higher block coefficient on a given waterline it is not unlikely that KB will also end up lower below the waterline, further decreasing metacentric height. This change is normally not that big and often comes with an decrease of the center of gravity height as well, offsetting this factor somewhat.
- Increasing the ships waterline size, especially the ships beam, will increase BM and with that the ships metacentric height.
- Raising the center of buoyancy (often visible in a reduction of midship coefficient) increases metacentric heights.
- Metacentric heights is between 1 and 2 meters for almost every ship of every size, apart from special cases (pontoons, crane barges, semi-submersibles, very small ships, etc) where there are special requirements or relatively large changes in center of gravity that have to be offset by a much larger stability margin.