An introduction to ship stability

Note: there may be words and definitions which might not be familiar to everyone in this article. Please take a look at the bucketeers glossary Bucketeers Glossary or contact acelanceloet on discord or by forum pm if any questions remain (which I will then answer and add to the bucketeers glossary or this article)

This article is written by J. Scholtens / acelanceloet to provide some insight in the stability of ships, how it impacts ship design and how to use some simple calculations and estimations to see if your shipbucket drawing would stay upright, safe and comfortable. Each section is in theory independent, you can read just the section of what you want to do (for example, estimate the center of gravity of an real ship so you can compare it with your AU design) but to fully understand what you are doing and why it works, it may be required to read the sections above it. That way, I hope that this article will be useful for the people who want to do full calculations, but also for the people who just want to do a quick estimate if their ship works. Unless stated otherwise, I will be using SI units (mostly meters).

Definitions

• The ship: the floating object we are doing these calculations for. I will be using ship, but a boat, bouy, submarine or a pontoon of course follows the same rules.
• 'K' : The zero point for the Metacentric height calculation. It can be chosen to be any point, as long as it is constant in the calculations. Normally, it is kept at the bottom of the ship, the keel, which is why the K is chosen for it's abbriviated form.
• 'G' : The Center of Gravity of the ship, or in other words the balancing point of all weights on the ship combined.
• 'B' : The Center of Bouyancy of the ship. This is the center of gravity of the water displaced by the ship, or in other words the centerpoint of the underwater volume of the ship.
• 'V' : The volume of the ship. Following archimedes' law, this is equal to the weight of the ship divided by the density of the water.
• 'KG' : The distance between K and G in vertical direction.
• 'KB' : The distance between K and B in vertical direction.

Archimedes' law: Why objects float

There is a direct relation between submerged volume and weight of an object. If a bucket of water is filled to the brim and a floating object is put in, some water will flow over the edge of the bucket. Interestingly, the weight of this water will be the same as that of the floating object. Due to the fact that the density of water is known, a relation between the displaced water and the submerged volume of the object can also be found. Because the floating object 'displacing' the water that otherwise would be in that location, a ships weight is often stated as displacement

The resulting formula is:

• displacement = underwater volume * water density

or in symbols

• Δ = V * ρ

Water density is 998 kg/m³ for fresh water and 1025 kg/m³ for salt water. Due to the closeness to 1000 of both values, for estimations displacement in cubic metres is often stated as being equal to displacement in metric tons. This of course isn't valid in detailed calculations, although for fresh water it is considered close enough in many cases.

Using Archimedes' law the submerged volume of a ship can be found if the weight is known, or a weight can be found when the volume is known. This forms the basis for the stability calculation: with this it is proven that displacing water by pushing something into it delivers an opposing force equal to the weight of the water it 'replaces'.

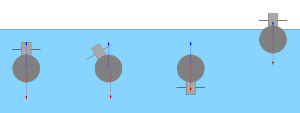
The simple case: Stability of an submerged object

Below the surface of the water, stability is relatively simple. The best example of this case is an submarine. In an object completely submerged in a single medium, it will be stable if the center of gravity is directly below the center of bouyancy. If the object starts to slant, the center of gravity moves to the side of the center of bouyancy, creating an counterforce that gets bigger the more the larger the angle of the object becomes. This counterforce reaches zero when the angle returns to zero. In that essence, the further below the center of gravity is below the center of bouyancy, the larger this counterforce becomes with every angle.

Submarines are well known for their uncomfortable motions at the surface. This can be explained when looking at the characteristics of objects floating at the surface.

Stability while afloat at the surface

a simple diagram of how the forces making an floating object more stable at the surface work. When centre of bouyancy and centre of gravity are in line, the objects floatation can be described just using archimedes' law. If you would split the object in half and put a lot more mass on one side, following archimedes' law one side would float higher as it gets lighter, the other would sink deeper as it carries more weight. The total bouyancy of both instances remains the same. The third situation is basically the same, but the object is attached together again. There is still one side floating up and one side laying deeper in the water when the mass is moved to one side, so the object now floats at an angle.

On the surface, the stability of an floating object follows the same laws as below the surface with one addition: the shape of the objects submerged volume changes as the object gets an angle. one side is lifted out of the water while the other is pushed deeper into it. The center of gravity moves over a bit to the low side, but the center of bouyancy does so too due to the loss of volume at the high side and the increase of volume at the low side. In other words: at the surface, as long as the shape of the waterline remains the same, the bigger the angle gets, the more the objects volume starts counteracting. So, a ship at the surface is a lot more stable then a submerged object.

To find out how stable, it is required to do some calculations, which can be found in the next paragraph. It is however possible to do some simple estimations:

• The lower the center of gravity, the higher the stability
• The lower the volume relative to the waterline area, the higher the stability.
• The higher the center of bouyancy, the higher the stability.
• The larger the ships beam, the larger the ships stability.

Calculating the metacentric height

To really compare a ships stability, it is required to do calculations though. The most important value to compare stability of ships is the metacentric height or GM. Metacentric height is a fictional turning point for the angling of the ship. The center of gravity of the ship can be considered a pendulum that is attached at this fictional point, the metacentre. This means that the higher this GM gets, the slower the ship angles and the more momentum is needed to get it to heel.

A high GM thus means that it is difficult to get the ship to heel over. Interestingly, GM doesn't scale linearly with ship size: a sailing yacht and a panamax container ship might have metacentric heights which are not very far apart. How to compare the requirements set for metacentric heights will be described in the paragraph #Stability requirements

The formulas used for the calculation of the metacentric height are the following:

• GM = BM + KB - KG

in which:

• BM = Iwp / V

BM is the distance between the Center of Bouyancy and is defined by the second moment of inertia of the shape of the waterline divided by the underwater volume of the ship. More about the second moment of inertia below. The BM is the reason the stability goes up if the volume of the ship is reduced without changing the waterline and also the reason why stability goes up when stability rises when the waterline area is increased without changing the ships volume.

The GM, KB and KG are described earlier on this page.

Second moment of Inertia of the ships waterline

The second moment of inertia of the waterline is the most complicated part of the stability calculation. It is a value for the waterline area and the distribution of that area. For simple shapes, a formula can describe it exactly:

• Rectangle: I_WP = 1/12 * L * B³
• Oval: I_WP = 1/4 * π * (0.5 * L) * (0.5 * B)³

The above formula's are valid for transverse stability. Longtitudinal stability uses the same formula's but of course a ship pitches a lot harder then it heels in most cases. Center of bouyancy, center of gravity and the volume remain the same, but the second moment of intertia is modified to perform this mechanic: the longtitudinal second moment of inertia is defined by moving the cubed factor to the length instead of the beam, so for the rectangle that results in:

• Rectangle: 1/12 * B * L³

In the table below a few waterline second moment of inertia formula's are coupled with an waterplane coefficient and a description of the hulls. They are all estimations so be careful when applying them to real designs but they will work to get an estimation of stability of a ship.

estimated second moments of intertia for common hull shapes

Shape / ship type	IWP =	Waterplane coefficient
Square pontoon	1/12 * L * B3	1.00
FPSO (rounded pontoon shape)	1/13 * L * B3	0.95
Heavy lift ship (sharp bow, parallel midship, broad transom stern)	1/15 * L * B3	0.85
Bulkcarrier (round bow, small transom stern)	1/16 * L * B3	0.82
Modern warship hull	Between 1/16 and 1/24 * L * B3	Between 0.84 and 0.72
Cruiser hull (sharp bow, small transom)	1/22 * L * B3	0.75
Semi-planing hull	1/22 * L * B3	0.75
Sailing yacht (sharp bow, sharp or rounded stern)	Between 1/20 and 1/26 * L * B3	Between 0.79 and 0.67
Container ship (sharp bow, small or no transom)	Between 1/22 and 1/26 * L * B3	Between 0.75 and 0.67
Planing hull	1/26 * L * B3	0.67
Pre-war destroyer hull	1/26 * L * B3	0.67

Note that the faster a ship will go (relative to it's size) the less the hull is optimised for stability and the more for speed, leading to a lower waterplane area second moment of inertia and with that to a lower BM.

The stability when the floating object gets an angle

The metacentric height defines how easy it is to get a ship from no angle to an angle. To make this fact useful, we have to be able to put an exact number on this 'resistance', what are the actual forces the ship will be able to handle with this stability, and what angle will this result in? To find that information, the righting arm calculation can be used.

The righting arm calculation

The righting arm calculation defines how much the ships centre of gravity has to move sideways to get the floating object to a certain angle. This calculation is generally considered valid at small angles (less then 7 degrees)

The formula used for the calculation of the righting arm is the following:

• GZ = GM sin φ

In the above formula, GZ or the "static lever of stability" is the distance (in the same units as the GM is described in) the centre of gravity has moved and φ is the resulting angle.

GZ can be used to describe a static force, such as the weight of the ship being offset from midship leading to an angle, but it can also be used to check the resulting angles of other forces. GZ is the lever that a force equal to the weight of the ship would need to reach an angle. A force equal to 1/10 the weight of the ship would have a lever 10 times the size of GZ to lead to the angle φ.

The reason the calculation is considered valid only at small angles, is because the calculation does not take into account the vertical movement of the Center of bouyancy (KG) resulting from the ships angle. There is another method to take this into account, called Scribantis formula. Usage of this method goes beyond the scope of this page.

Hull shape effects

Apart from the actual calculation, there is one other issue that can make the calculation less valid: the shape of the ships hull. The calculation 'assumes' the hull of the ship goes straight up from the waterline. This isn't a problem because most ships flare out somewhat, at the very least at the bow and stern, which means the stability is actually slightly higher than the calculation results describe. Because of that it is considered a safe error. The shape of the hull has to be taken into account though, and on hulls that vary a lot from the assumed shape (for example very flared out or tumblehome hulls) this might result in a ship not meeting requirements or requiring corrections. In the maritime industry this is done by having computer programs calculate the stability. The metacentric height at angle = 0 doesn't change, but at other angles a correction might have to be added for the results to be accurate. Using a computer program it is possible to get far more accurate results for small angles as well, but the need for the formula's described above is there for quick estimations and to check computer results: The computer is probably more accurate, but is possibly very wrong if errors are made in the input.

The stability curve

As a floating object is rarely completely level in the water, it is needed to look at more than just the metacentric height and the GZ if φ is zero. Because of this, the so-called stability curve is drawn for every ship (and often multiple for the various load conditions). The stability curve is a graph of GZ set against the heeling angle φ. The GZ is calculated for every angle that is important. What is important is defined by the type and design of the ship: if a ship floods when it is angled over 15 degrees, then there is very little point to draw a stability curve any further then that as the conditions change after that point. If the ship is a self-righting design, the full 180 degrees of angle (or sometimes even 360 degrees) are important.

As long as the sides of the ship are going straight up, the stability curve will follow the values from GM sin φ quite closely. Because of this it is said that the angle of the curve at φ = 0 is defined by the GM. The big changes (apart from some effects from the shape of the hull) comes from the shape of the waterline abruptly changing shape, such as the point the deck enters the water or the bilge comes out of the water. The maximum GZ in most cases occurs somewhere between the point that the bilge comes out of the water and the point the deck enters the water. Because of this, block coefficient, hull depth and draft have quite an impact on the stability curve of a ship.

The largest GZ is the largest righting arm the ship can take statically. If the ship passes this angle of maximal GZ there is less and less force to push it back upright. Removal of the force causing this angle might however let it return to the previous condition. Once the GZ reaches zero, the ship will capsize.

Stability requirements

Stated above is that the stability of a floating object is defined by the metacentric height and the stability curve. Generally speaking, any that has a metacentric height that is positive is safe. To make sure the floating object is safe, some more things have to be kept in mind though!

Load conditions and damaged stability

Most floating objects aren't static. Any pontoonbridge, rowing boat, cargo ship or navy ship, for example, performs a function other then just carrying it's own weight in water, such as carrying cargo or transporting people. This often leads to different conditions in which the stability has to remain positive. These conditions can be load conditions (full load, standard, light ship and everything in between), forces on the floating object (cranes, shifting cargo, water on the deck, ice on the deck) or even a condition where the ship is holed and certain parts of the ship are flooded. Late in the ship design process, these conditions are all calculated and it is checked which conditions could happen at the same time. This will then pose limits on the operational conditions of the ship. Early in the design however, the stability will just be checked for the common load conditions and it is checked if there are no special conditions that have to be taken into account, such as for example large cranes or special cargoes. Most of the time a stability margin at this stage is chosen by comparing to reference ships.

Damaged stability and everything needed to calculate those conditions is beyond the scope of this page.

Stability and the ships motions

It is important to keep in mind what effect the stability will have on the ships motions. As discussed above, the higher the metacentric height, the more force is needed to get the ship to an angle. This means a very stable ship will be hard to get to an angle, so when forces act on it (waves, wind, etc) a ship will heel very little. In effect, the higher the stability, the smaller the angles the ship reaches in given conditions, which means the motion will be smaller but quicker. This in turn leads to high accelerations and unexpected motions which can lead to safety issues and motion sickness of the crew. A low stability on the other hand will lead to higher angles of heel (even when the ship is perfectly safe) which can lead to unsafe feeling of the crew and loss of footing or the shifting of cargo. In other words: the conditions the vessel has to operate in have to be kept in mind for the stability requirements.

Most manned vessels have a metacentric height of between 1 and 1,5 meters. This is true for ships from small rowing boats all the way to huge aircraft carriers, as the small craft have far more sudden centre of gravity differences (somebody stepping on board) then the large ships.

In addition to being the forces that move ships, if a ship is in waves the shape of it's underwater hull and waterline will also change. This sometimes has a positive and sometimes a negative effect. The stability has to have some margins to be able to handle these conditions.

The margin of stability for future upgrading

Ships tend to be heavier and get more topweight over their operational service life. This is especially true for navy ships. Because of this, ships are designed with some margins in displacement and stability both to make sure they will be safe over their entire service life, or said better that they can be upgraded or modernised without being restricted by the silly thing called safety and comfort. A ship that is not meant to be upgraded over its service life will because of this have far less restrictions on it's GM then a ship designed to be converted and modernised over time. Because of this, a lower GM was for example acceptable for the Ticonderoga class then on the Spruance class. Similarly, it has been seen that these margins have been made smaller on repeat ships that had small modifications as "a mature design has less chance to have unforeseen weight increases then one still in the design process". Apparently, the margins also exist for unforeseen increases in topweight even when the ship is not yet build.

The requirements on stability summarised

All in all, the ships metacentric height requirements are defined by:

• Increases in centre of gravity height. (which lower GM by increasing KG.)
• Increases in ship weight. (Which lower GM by decreasing BM.)
• Reduced stability due to flooding.
• Reduced stability due to waterline shape modifications. (Reducing GM by decreasing BM.)
• The motions of the ship keeping the crew in conditions in which they can work.
• The loss of stability by not having the entire hull under water in different wave conditions.
• Margins to handle all load conditions and shifting of cargo.
• Any special operations the floating object has to perform to fulfil it's purpose.

Estimating the center of gravity of an existing ship using the stability

Using the above formula’s and information, it is possible to estimate the stability of any ship design. However, one factor is often somewhat hard to estimate, which is the height of the centre of gravity. There are 2 ways to estimate the center of gravity of a ship:

• Take the center of gravity height above the keel of every component and multiply this with the weight of this component. Then take the sum of all multiplied components and divide this by the total weight ( = the displacement of the ship)
• Estimate (possibly by using the above method) how the center of gravity differs from a reference ship of which the metacentric height and dimensions are known. Then reverse engineer the metacentric height of that ship (calculating BM and estimating KB) to find KG.

The last method is one more commonly used in initial or conceptual design (if the center of gravity cannot be estimated from earlier similar projects, that is)

The formula to be used to find the KG is:

• KG = BM + KB – GM

Rules of thumb for modifying a ships stability

It is not always necessary to make a full calculation of a ships stability. For small changes to an calculated or existing design or to the load conditions of a ship, some rules of thumb can be followed to find the effects on the ships stability.

• Any change in the height of the center of gravity will have an opposite effect on the metacentric height. So moving the center of gravity one meter up means the metacentric height comes down one meter.
• On a given waterline shape and size, an increase of block coefficient (more volume under water) means an lower BM so a reduced metacentric height. With an higher block coefficient on a given waterline it is not unlikely that KB will also end up lower below the waterline, further decreasing metacentric height. This change is normally not that big and often comes with an decrease of the center of gravity height as well, offsetting this factor somewhat.
• Increasing the ships waterline size, especially the ships beam, will increase BM and with that the ships metacentric height.
• Raising the center of buoyancy (often visible in a reduction of midship coefficient) increases metacentric heights.
• Metacentric heights is between 1 and 2 meters for almost every ship of every size, apart from special cases (pontoons, crane barges, semi-submersibles, very small ships, etc) where there are special requirements or relatively large changes in center of gravity that have to be offset by a much larger stability margin.

Conclusion

With the above information and calculations it is possible to check, judge and compare the stability of any floating object. It is written in a way that it should be possible to use just the information needed and use the rest as background. Because of that this document goes far more in-depth then most people will need.

This is mentioned a few times throughout the page, but there is one thing important when using this information: The only way to properly use this information is by looking at real ships. The calculations are a tool for analysis, both of existing ships and new designs. This is how they should be used in Shipbucket as that is how they are used in the maritime industry as well.

Have fun using this information and if there are any questions or issues, let J. Scholtens / acelanceloet know by pm on discord or on the shipbucket forums.