Shading guide
Because most Shipbucket images only consist of a single side view, it becomes necessary to use shading to depict curved surfaces, like gun barrels, funnels, barbettes, and the hull below the waterline. This page collects advice on shading rules, how they have evolved, and some rules-of-thumb you can use to calculate how much of an area to shade.
Note that this is meant as a general article for shading rules. Feel free to fill in the blank sections or add new ones, with or without diagrams.
Contents
Basic shading rules
Basic guidelines on shading can be found in the shading section of the official Shipbucket style guide.
On a standard Shipbucket starboard-side view (bow pointing right), the light source comes from the top of the canvas and the right of the canvas. For top views, fore/aft views, and left-facing side views, there is currently no universal Shipbucket standard; these views are rare enough that a few different approaches exist.
Shadows and overhangs
Shading cylinders
Cylinders often appear on a Shipbucket drawing: they often show up in features like masts, funnels, barbettes, conning towers, fire-control towers, AA gun tubs, torpedo tubes, and propeller shafts. You can also apply the advice in this section to curved corners of the superstructure, where the radius of the curve is one-half the diameter of a cylinder.
Remember that the light comes from the top and right of the canvas. On a horizontal cylinder like a gun barrel, shading should be lightest on top, base shade in the middle, and darkest on the bottom. On a vertical cylinder like a mast, shading should be lightest on the right, base shade in the middle, and darkest on the left. Some old drawings, like Psilander's, have the shading get darker at both sides of the cylinder; this is no longer considered to be a valid or standard Shipbucket drawing style.
Simple rules of thumb
Note: the numbers below include black outlines as part of the total. So a cylinder 5 pixels in diameter is (1px blk + 1px shade 1 + 1px base + 1px highlight + 1px blk).
When drawing a small cylinder 5-9 pixels in diameter, the standard approach is to use one line of highlight on either end. This is a little bit more than what the rules of thumb below request, but cylinders over 5px in diameter must have shading at both sides to show their rounded shape, so here, the exaggerated shade and highlight are acceptable and even required.
Where things get trickier is with larger cylinders, especially barbettes, funnels, and conning towers. The table below reports rules of thumb for shading these structures, where D represents the diameter of the cylinder, including black lines.
With 45-degree shading rules
- Highlight: 0.15 × D
- Base: 0.7 × D
- Shade: 0.15 × D
You can speed this up by using the process below. 1. Draw the sides of your cylinder as black lines on a white background. 2. Drag a box to measure the diameter between those lines, including both lines. 3. Multiply that diameter by 0.147. Round to the nearest whole pixel. 4. Drag a box that wide from the outside edge of the cylinder's right or top line. 5. Fill that box with the highlight shade. 6. Repeat for the cylinder's bottom or left line. 7. Fill that box with shade 1.
With 30/60-degree shading rules
- Highlight 2: 0.07 × D
- Highlight 1: 0.18 × D
- Base: 0.5 × D
- Shade 1: 0.18 × D
- Shade 2: 0.07 × D
A longer explanation
"But teacher, when are we ever gonna use this stuff in real life?" --Some of you, in high school, probably
Some of you, seeing the numbers above, might want to know the full explanation, especially given the degree of precision. The answer lies in the fact that a perfect cylinder, seen from the end, is a circle, and the point at which the outer surface of the circle transitions from 59.999 degrees to 60.001 degrees can be understood as a tangent line, which forms a right angle to the radius of the circle, at an angle of 60 degrees from the line pointing toward the viewer.
That's right: shading is a trigonometry problem.
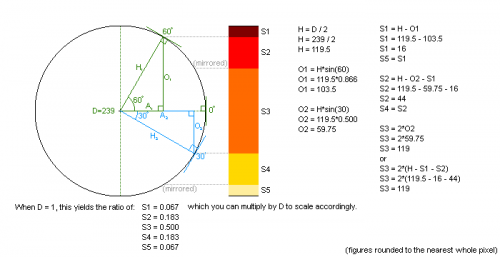
The diagram at right shows the full guts of a math problem that asks you to solve for the shading zones when using a 60/30 shading rule. Some of you, at least those who attended Anglophone high schools, might remember SOHCAHTOA:
- Sine = Opposite side over Hypotenuse
- Cosine = Adjacent side over Hypotenuse
- Tangent = Opposite side over Adjacent side
So O1 is cos(60), and O2 is cos(30). You can then subtract these from the radius of the circle, which is half the diameter, in this case 239 pixels including the line pixels. The hypotenuse is simply the radius drawn to any given point, so H1 = H2 = R = D/2. The rest of the math follows from there; remember that visually, you are mapping the zones between the tangent points, and you are getting those zones via different subtraction combinations of the radius and the "O" lines inside the circle.
There are of course simpler ways to calculate and represent this. A very slick rule of thumb when using the 45-degree shading rule is that cos(45) times the diameter (aka, 0.707 times the diameter) is equal to the width of the central base-shade zone, and you can then fill in the light and dark zones on either side.
A keen observer will note that you can modify this approach to apply to any shading rule, not just the common 45 or 30/60 rules. Rule-based shading lines at 15, 75, 37.5 degrees, etc., are now possible.
An even keener observer will note that this trigonometric scaling approach can also be used to assist in drawing a part, turret, or entire vehicle that is shown at an angle relative to the canvas. But this guide covers shading only.